L’algoritmo Bubble Sort è basato sullo scambio di elementi adiacenti. Ogni coppia di elementi adiacenti viene comparata e invertita di posizione, se il primo è più grande del secondo. Quando questa operazione è stata ripetuta per tutti gli elementi, si ha che l’elemento più grande si trova in fondo, a destra, della sequenza considerata.
Dopodiché, si ripete questa procedura sugli elementi rimanenti, togliendo elemento più grande trovato prima.
L’algoritmo, iterando più volte questi passaggi, fino a quando non ci saranno scambi. Allora l’array ottenuto sarà ordinato.
Deve il suo nome al modo in cui gli elementi vengono ordinati ossia quelli più piccoli “emergono” verso un’estremità della lista, così come fanno le bolle gassose in un bicchiere di acqua minerale; al contrario quelli più grandi “sprofondano” verso l’estremità opposta della sequenza.
Esempio
Abbiamo un array A = {3,5, 2, 4, 1} su cui applichiamo il bubble sort:
1. A = {3,5, 2, 4, 1} → A = {3,5,2, 4, 1} → A = {3, 2,5,4, 1} → A = {3, 2, 4,5,1} → A = {3, 2, 4, 1 | 5}
2. A = {3,2, 4, 1 | 5} → A = {2,3,4, 1 | 5} → A = {2, 3,4,1 | 5} → A = {2, 3, 1 | 4, 5}
3. A = {2,3, 1, | 4, 5} → A = {2,3,1 | 4, 5} → A = {2, 1 | 3, 4, 5}
4. A = {2,1 | 3, 4, 5} → A = {1, 2, 3, 4, 5}
Notare che, alla fine di ogni iterazione, l’elemento più grande del sottoinsieme ancora da ordinare, finisce in fondo alla sequenza, nella sua posizione definitivamente corretta, mentre la sottosequenza ancora in disordine si riduce di volta in volta di un elemento.
Codificando il Bubble Sort si ha:
1: flag = 1 2: stop = n −1 3: fintanto che flag = 1 ripeti 4: flag = 0 5: per i = 1, 2,...,stop ripeti 6: se ai > ai+1 allora 7: scambia ai e ai+1 8: flag = 1 9: fine-condizione 10: fine-ciclo 11: stop = stop −1 12: fine-ciclo
In Java si ha:
int[] v = { 2, 4, 7, 3, 5 };
boolean scambiFatti= false;
for (int i = v.length - 1; i > 0; i--) {
for (int j = 0; j <i; j++) {
if (v[j] > v[j + 1])// inverti
{
int tmp = v[j];
v[j] = v[j + 1];
v[j + 1] = tmp;
scambiFatti = true;
}
}
if(!scambiFatti) {
break;
}
}
for (int i = 0; i < v.length; i++)
System.out.println(v[i]);
Notare che il Bubble Sort corregge il difetto principale del selection sort, ossia il non accorgersi se l’array, a un certo punto, è già ordinato.
Anche in questo caso abbiamo due cicli annidati, ma, stavolta, l’algoritmo usa la variabile flag per terminare l’esecuzione, nel caso in cui l’insieme risulti ordinato.
Nel caso migliore, ossia quando l’insieme è già ordinato, l’algoritmo esegue un’unica scansione, quindi il numero di operazioni eseguite sarà dell’ordine di n.
Nel caso peggiore, alla prima iterazione vengono eseguite dunque sono necessarie n − 1 iterazioni del ciclo esterno per ordinare l’intera sequenza. Alla seconda n-2, e cosi via. Quindi il numero di operazioni svolte è:
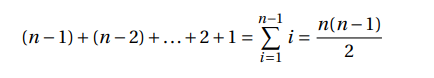
Concludendo la complessità computazionale del Bubble Sort è di O(n 2 ).
