Il Merge Sort, inventato da John Von Neumann nel 1945, è molto simile al Quick Sort, ma l’elemento pivot, in questo caso, viene scelto sempre nel centro.
L’idea principale è che, avendo due array ordinati, è molto semplice fonderli in un unico array ordinato. Inoltre, un’array di un elemento è sempre ordinato.
Unendo questi concetti, si ha un algoritmo che, dopo aver suddiviso ricorsivamente l’array iniziale A in n sotto-array, costituiti da un solo elemento, fonde i sotto-array e fino a ottenere un’unico array ordinato.
Codificando il tutto si ha:

L’algoritmo è diviso in due metodi: il MergeSort e il Merge.
Il MergeSort riceve in input l’array A e i due indici p e r, che permettono di identificare l’elemento ap e l’elemento ar, ossia il primo e l’ultimo elemento.
Esso divide, ricorsivamente, l’array in due parti, in modo tale che i due sotto-array ottenuti abbiano un ugual numero di elementi (a meno di uno, nel caso di insiemi con cardinalità dispari). Durante la suddivisione l’array non viene modificato.
La riga 2 del codice individua l’indice q dell’elemento che si trova a metà dell’array.
Dopodiché, viene chiamato ricorsivamente il metodo MergeSort sulla prima metà e sulla seconda metà.
La procedura si ripete ricorsivamente fino a quando si arriva ad array composti da un solo elemento, ossia quando p = r .
A questo punto, entra in gioco la procedura Merge, che provvede alla “fusione” dei due array A0 = {ap ,ap+1,…,aq } e A 00 = {aq+1,aq+2,…,ar }.
La fusione avviene scansionando in parallelo entrambe le sequenze (ciclo principale, righe 2–8), e copiando nell’insieme di appoggio B l’elemento minore tra ai e aj.
Nel caso in cui una delle due sequenze è stata copiata completamente in B, la procedura prosegue copiando in B gli elementi rimanenti dell’altra sotto-sequenza. Infine gli elementi ordinati dell’insieme B vengono copiati nuovamente in A, ottenendo alla fine l’ordinamento di A.
Esempio
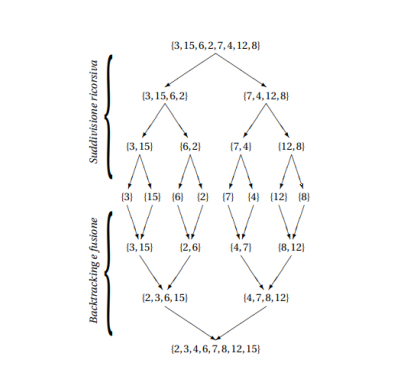
La complessità computazionale del Merge Sort è sempre O(n log2 n), a prescindere dai dati in input, quindi ha la più bassa complessità degli algoritmi visti fino ad ora.
Gli svantaggi sono che necessita di un vettore di appoggio ed effettua spostamenti anche nel caso in cui il vettore di partenza è già ordinato
