L’algoritmo di ordinamento InsertSort (ordinamento diretto) nasce dal concetto che per ordinare un array ordinato è sufficiente costruirne uno nuovo ordinato, inserendo gli elementi al posto giusto da subito. Nella pratica, non è necessario crearne uno nuovo ma dividere quello esistente in due parti, una ordinata e l’altra no.
Esempio:
Vogliamo ordinare l’insieme A = {5, 3, 2, 1, 4}.
Iterazione 1. A = {5 | 2, 3, 1, 4} → A = {2, 5 | 3, 1, 4}
Iterazione 2. A = {2, 5 | 3, 1, 4} → A = {2,3, 5 | 1, 4}
Iterazione 3. A = {2, 3, 5 | 1, 4} → A = {1, 2, 3, 5 | 4}
Iterazione 4. A = {1, 2, 3, 5 | 4} → A = {1, 2, 3,4, 5}
Codificando l’Insert Sort abbiamo:
1: per i = 2, 3,...,n ripeti 2: k = i −1 3: fintanto che k ≥ 1 e ak > ak+1 ripeti 4: scambia ak e ak+1 5: k = k −1 6: fine-ciclo 7: fine-ciclo
In Java diventa:
public void insertionSort(int [] array) {
for(int i = 1; i < array.length; i++) {
int x = i;
int j = i-1;
for(; j >= 0; j--) {
//Scambiamo l'elemento in posizione x fino a quando non raggiunge
//la posizione corretta nel sotto-vettore, cioé quando
//non é verificata piú questa condizione
if(array[j]>array[x]) {
int k = array[x];
array[x] = array[j];
array[j] = k;
x = j; //La sua nuova posizione nel sotto-vettore
} else break; //Significa che l'i-esimo elemento è nella sua giusta posizione
//quindi possiamo terminare l' iterazione
}
}
}
Nel caso migliore, ossia quando l’array è già ordinato, il numero di operazioni svolte dall’algoritmo è dell’ordine di n.
Nel caso peggiore, il numero di operazioni eseguite dall’algoritmo è:
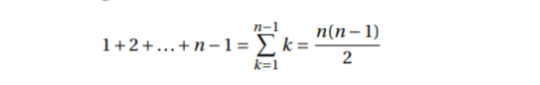
La complessità dell’algoritmo nel caso peggiore è quindi O(n 2 ).
